Theoretische Codes. Was soll das sein?
Öfter mal liest man in Werbung oder Beschreibungen von mechanischen Schlössern den Begriff „theoretische Codes“, „theoretische Verschiedenheiten“ oder auch „theoretische Permutationen“. Über 200.000 theoretische Codes, was bedeutet das?
Nun, da es sich um Werbung handelt, hat man erst mal hat man den Verdacht, dass die Zahl der wirklichen Code-Verschiedenheiten unter 200.000 liegt. Das ist auch so. Der theoretische Wert ist nämlich einfach rechnerisch ermittelt:
Bei Kombinationsschlössern – Anzahl Teilstriche hoch Anzahl Code-Scheiben
Bei Schlüsselschlössern – Anzahl Schnitttiefen hoch Anzahl Einschnitte
Wirkliche Aussagekraft über die Sicherheit eines mechanischen Schlosses geben diese Zahlen aber nicht, denn die Eigenschaften der Mechanik bleiben dabei völlig unberücksichtigt.
Wenn man bei einem 3-Scheiben Zahlenkombinationsschloss beim Einstellen der letzten Scheibe einen halben oder ganzen Teilstrich zu weit dreht, wird man feststellen, dass das Schloss trotzdem öffnet. Das ist (bis zu einem gewissen Maß) auch OK und das Schloss erfüllt wahrscheinlich die Forderung der Norm von 100.000 Verschiedenheiten. Es ist halt nur Unsinn im Zusammenhang mit Sicherheit den theoretischen Wert von 1 Mio zu nennen.
Fertigungstoleranzen
Alle mechanischen Schlösser bestehen aus mechanischen Teilen, die ineinandergreifen. Und jedes Teil hat entsprechende Fertigungstoleranzen. Je präziser die Teile gefertigt sind, desto mehr wirkliche Code-Verschiedenheiten können erzielt werden. Anders ausgedrückt: Je wobbeliger der Schlüssel oder der Zahlenknopf sich beim Drehen anfühlt, desto weniger reale Codes hat das Schloss.
Gewolltes Spiel
Es ist aber auch ein gewisses Maß an Spiel bei den Teilen notwendig um zu gewährleisten, dass das Schloss auch dann noch funktioniert, wenn etwas Staub eingedrungen ist oder nach Jahren Gebrauch Korrosion angesetzt hat. Sie ahnen schon, auch dies geht zu Lasten der realen verfügbaren Codes.
Bedienerfreundlichkeit
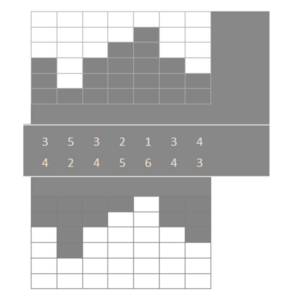
Nehmen wir als Beispiel einen Doppelbart-Schlüssel mit 7 Einschnitten, die jeweils 6 verschiedene Tiefen haben können. Die theoretische Zahl an Kodierungen beträgt demnach 6 hoch 7 = 279.936. In Wahrheit werden aber viele der theoretisch möglichen Schlüssel niemals hergestellt. So in etwa stellt man sich den Schlüssel vor:
Niemand möchte jedoch einen der folgenden Schlüssel haben:
Die entsprechenden Schlösser wären leicht zu knacken und die einzelnen Zinken bei solchen Schlüsseln würden sehr schnell verbiegen oder abbrechen. Tatsächlich sind in unserem Beispiel fast die Hälfte der theoretischen Schlüssel in der Realität aus verschiedenen Gründen ungeeignet.
Ein anderes Beispiel
Sie stellen bei einem Kombinationsschloss den Code ein und schauen dabei diesmal etwas schräg auf den Zahlenknopf. In der theoretischen Welt dürfte das Schloss wegen der Parallaxe nicht aufgehen. In Realität tut es das aber doch, weil die Breite des Steges am Einfallhebel viel geringer ist als die Breite des Einschnitts in der Code-Scheibe (Wie funktioniert ein Zahlenkombinationsschloss? Hier mehr erfahren). Der englische Fachbegriff dafür lautet „dialing span“ und gibt an, wieviel Ungenauigkeit das Schloss beim Einstellen des Codes erlaubt. Aber: Je höher die Bedienerfreundlichkeit, desto weniger bleibt von den theoretischen Code-Verschiedenheiten übrig.
Fazit
Bei mechanischen Schlössern ist die Angabe von theoretischen Codes dumm und irreführend. Nur bei elektronischen Schlössern stimmen hier Theorie und Realität überein.